Background part two. Traction circle: your tyres dictate how quickly you can stop More reading: Brian Beckman Next / Back

The Traction Circle is a brilliantly simple way of understanding how your tyres generate grip. It is very useful in understanding that there is a 'traction budget' on your tyres as you enter a bend - if you attempt to accelerate or decelerate and you are already at the tyre's limit of lateral adhesion whilst cornering, the tyres will simply exceed their traction budget, and slide: and you'll be going gardening in your car viewing the way ahead in your rear view mirror…

The traction circle is also helpful in understanding one of the key concepts in how quickly you can brake in your car. Brian Beckman describes this in more detail here: http://www.miata.net/sport/Physics/07-Circle.html but we'll go through it in a little detail here as well. As in the previous background page, we'll be using our good friend's - Sir Isaac Newton's - equations again. But first is the equation that governs the force that is required to slide an object over any surface:

Where F_max is the maximum force that a tyre can generate under acceleration or deceleration before slipping. This force is proportional with the coefficient of friction between the tyre and the road surface (m), and the force pushing the tyre down onto the road (M, which is related to the weight of the vehicle). So the heavier the object (car in this case), the more lateral force is required to push on it to make it slide.

So what happens at maximum deceleration? That will occur when the force the tyre can generate is F_max, = mW, where the weight over that wheel (W) acting on the tyre will be f_amg

All the mass units are cancelled out! Therefore, the maximum deceleration (or acceleration) that any tyre can generate is dictated purely by the coefficient of friction (m) - a constant! It doesn't matter therefore if you are driving a light-weight Caterham 7 or a 2-tonne Bentley Continental GT, if they are on the same tyres, the maximum retardation either can generate is going to be the same!

Figure 1: The Traction Circle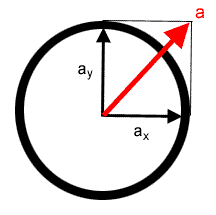 The traction circle represents the maximum acceleration, in ANY direction, that can be applied to the tyre before slip ensues. Thus the radius of the circle is amax. If acceleration is applied in two directions at the same time (as here, ax and ay, then the summation of the vector MUST not exceed amax or less the tyre WILL slide.

If we take the concept a little further, we can see that a_max applies equally in all directions the tyre can move over the two-dimensional surface of the ground. Thus, by Pythagorean theory,

a_max=sqr(a_x²+a_y²)

- which neatly describes a circle (figure 1): thus we have derived the traction circle! This equation elegantly tells us that if you can keep the acceleration in one direction only, you can maximise the acceleration/ deceleration the tyre is able to apply. If however one applies near maximal acceleration in both directions at the same time, the acceleration will exceed what the tyre is capable is handling (the red arrow in figure 1), and it will simply slide: hence the reason why we don't tend to brake in corners.

What does all this mean in terms of brake design? Well the knock out punch is that it matters not how HUGE your brakes are, you simply are not going to be able to decelerate faster than the point of maximum adhesion of the tyre - which on a road tyre means 0.9-1.0G.

This neatly leads us into the next part of the discussion - dispelling the myth that big brakes must mean that you stop more quickly.... NEXT page